Question

The depth of the water at the end of a pier changes periodically along with the movement of tides. On a particular day, low tides occur at 12:00am and 12:30pm, with a dept of 2.5 m, while high tides occur at 6:15am and 6:45pm, with a depth of 5.5 m. Let t=0 be 12:00 am. Which periodic function, since or cosine would be simpler model for the situation?

Answer 1

`x(t) = -1.5cos((2 \pi t)/(12.5)) + 4`

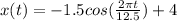
Explanation:

General formula

`x(t) = -Acos((2 \pi t)/(T)) + B`

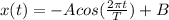
First transform data

12:00 am -> t=0 -> x=2.5

6:15 am -> t=6.25 -> x=5.5

12:30 pm -> t=12.5 -> x=2.5

6:45pm -> t=18.75 -> x=5.5

Period (T) is the time between two equal values of x.

t=0 -> x=2.5

t=12.5 -> x=2.5

t=6.25 -> x=5.5

t=18.75 -> x=5.5

T = 12.5 - 0 = 18.75 - 6.25 = 12.5

B is the shift of the cosine function with respect to y-coordinate. It is halfway between maximum and minimum values of the function

B = (5.5 + 2.5)/2 = 4

The amplitude (A) is the distance from the highest point to B

A = 5.5 - 4 = 1.5

Therefore, the correlation is

`x(t) = -1.5cos((2 \pi t)/(12.5)) + 4`

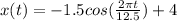
Model verification

x(0) = -1.5 + 4 = 2.5

x(6.25) = 1.5 + 4 = 5.5

x(12.5) = -1.5 + 4 = 2.5