Question

Find the distance formula ​

Answer 1

`\mathfrak{Distance \: between \: two \:points}`

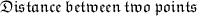
The distance between two points
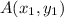`A(x_1,y_1)` and
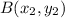`B(x_2,y_2)` is given by the formula,

`AB= √((x_2-x_1)^2+(y_2-y_1)^2 )`

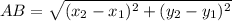
Proof: Let X'OX and YOY' be the x-axis and y-axis respectively. Then, O is the origin.

Let
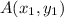`A(x_1,y_1)` and
`B(x_2,y_2)`

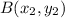
be the given points.

Draw AL perpendicular to OX, BM perpendicular to OX and AN perpendicular to BM

Now,
`OL=x_1,OM=x_2,AL=y_1 \: and \: BM=y_2`

`\therefore{AN=LM=(OM-OL)=(x_2-x_1)}`

`\: \: \: BN=(BM-NM)=(BM-AL)=(y_2-y_1)`

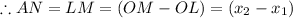
In right angled triangle
`\triangle \: ANB`,by Pythagorean theorem,

We have,

`\: \: \: AB^2=AN^2+BN^2`

`or,AB^2=(x_2-x_1)^2+(y_2-y_1)^2`

`\therefore \: AB= √((x_2-x_1)^2+(y_2-y_1)^2)`

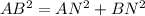
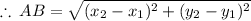
Thus ,the distance between the points A(x_1,y_1) and B(x_2,y_2) is given by,

`\implies \boxed{AB= √((x_2-x_1)^2+(y_2-y_1)^2) }`

Answer 2

d=(x^2-x^1)+(y^2-y^1)^2