Question

If $500 were to compound

continuously at a yearly interest
rate of 7%, what would the total
amount be after 10 years?
$[?]
Round your answer to the nearest hundredth.

Answer 1

Total amount: $1,006.88

Explanation:

Given the principal amount of $500 that is compounded continuously for 10 years at an annual interest rate of 7%:

We can use the following Continuous Compound Interest Formula to determine the future value of the total amount of investment:

`\displaystyle\mathsf{\Bigg\ Continuous\:Compound\:Interest:\quad\ A\:=\:Pe^((r*\\ t))}`

where:

A = The future value of the total amount in the account at the end of "t" number of years

P = Present value of the principal amount invested = $500

e = constant (base of the exponential function) ≈ 2.71828

r = Annual interest rate = 7% or 0.07

t = time (in years) = 10 years

Solution:

Substitute the given values into the Continuous Compound Interest Formula:

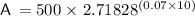
`\displaystyle\mathsf{\Bigg\ Continuous\:Compound\:Interest:\quad\ A\:=\:Pe^((r*\\ t))}`

`\displaystyle\mathsf{A\:=\:$500\:*\ 2.71828 ^((0.07*\\ 10))}`

`\displaystyle\mathsf{A\:=\:$500\:*\ [2.71828 ^((0.70))]}`

`\displaystyle\mathsf{A\:=\:$500\:*\ 2.013752707}`

`\displaystyle\mathsf{A\:=\$1,006.88}}`

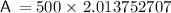
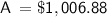
Therefore, the total amount accumulated after continuously compounding the principal investment for 10 years is $1,006.88. This includes the principal amount invested, $500, plus the interest accrued of $506.88.