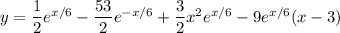Question

Solve the differential equation by variation of parameters, subject to the initial conditions y(0) = 1, y'(0) = 0. 36y'' − y = xex/6

Answer 1

The homogeneous ODE

`36y''-y=0`

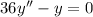
has characteristic equation

`36r^2-1=0`

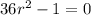
with roots at
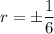`r=\pm\frac16`, and admits two linearly independent solutions,

`y_1=e^(x/6)`

`y_2=e^(-x/6)`

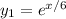
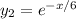
as the Wronskian is

`W(y_1,y_2)=\begin{vmatrix}e^(x/6)&e^(-x/6)\\\\\frac16e^(x/6)&-\frac16e^(-x/6)\end{vmatrix}=-\frac13\\eq0`

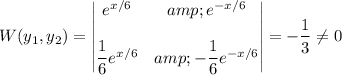
Variation of parameters has us looking for solutions of the form

`y_p=u_1y_1+u_2y_2`

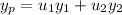
such that

`u_1=-\displaystyle\int(y_2xe^(x/6))/(W(y_1,y_2))\,\mathrm dx`

`u_2=\displaystyle\int(y_1xe^(x/6))/(W(y_1,y_2))\,\mathrm dx`

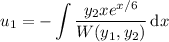
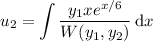
We have

`u_1=\displaystyle3\int x\,\mathrm dx=\frac{3x^2}2`

`u_2=\displaystyle-3\int xe^(x/3)\,\mathrm dx=-9e^(x/3)(x-3)`

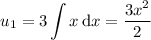
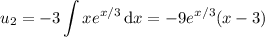
and we get

`y_p=\frac{3x^2e^(x/6)}2-9e^(x/6)(x-3)`

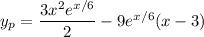
The general solution is

`y=y_c+y_p`

`y=C_1e^(x/6)+C_2e^(-x/6)+\frac{3x^2e^(x/6)}2-9e^(x/6)(x-3)`

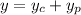
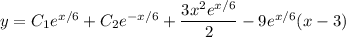
The initial conditions tell us

`\begin{cases}1=C_1+C_2+27\\\\0=\frac{C_1}6-\frac{C_2}6-\frac92\end{cases}\implies C_1=\frac12,C_2=-\frac{53}2`

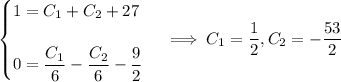
so that the particular solution is

`y=\frac12e^(x/6)-\frac{53}2e^(-x/6)+\frac32x^2e^(x/6)-9e^(x/6)(x-3)`