Answer:
a.

Explanation:
The given equation is
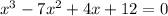
To find all real solutions using the x-intercept method, we to graph the corresponding function using a graphing tool.
The corresponding function is;
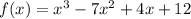
The real solutions to
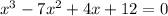 , are the x-intercepts of the graph of the corresponding function.
, are the x-intercepts of the graph of the corresponding function.
From the graph the x-intercepts are
(-1,0),(2,0) and (6,0).
Therefore the real solutions are
