Answer:
False
Explanation:
We have the serie:
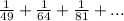
To test whether the series converges or diverges first we must find the rule of the series
Note that:
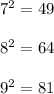
Then we can write the series as:
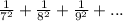
Then:
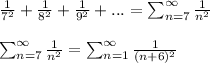
The series that have the form:
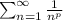
are known as "p-series". This type of series converges whenever
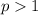 .
.
In this case,
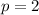 and
and
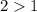 . Then the series converges
. Then the series converges