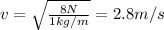Question

Part 1: A rope has one end tied to a vertical support. You hold the other end so that the rope is horizontal. If you move the end of the rope back and forth with a frequency of 4 Hz, the transverse wave you produce has a wavelength of 0.5 m. What is the speed of the wave in the rope?a. 0.13 m/sb. 8 m/sc. 2 m/sd. 4 m/sPart 2: A rope with a mass density of 1 kg/m has one end tied to a vertical support. You hold the other end so that the rope is horizontal and has a tension of 4 N. If you move the end of the rope back and forth, you produce a transverse wave in the rope with a wave speed of 2 m/s. If you double the amount of tension you exert on the rope, what is the wave speed?a. 2.8 m/sb. 1.0 m/sc. 2.0 m/sd. 0.25 m/se. 4.0 m/s

Answer 1

1) c. 2 m/s

Step-by-step explanation:

The relationship between frequency, wavelength and speed of a wave is

`v=\lambda f`

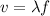
where

v is the speed

`\lambda` is the wavelength

f is the frequency

For the wave in this problem,

f = 4 Hz

`\lambda=0.5 m`

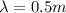
So, the speed is

`v=(0.5 m)(4 Hz)=2 m/s`

2) a. 2.8 m/s

The speed of the wave on a string is given

`v=\sqrt{(T)/(\mu)}`

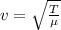
where

T is the tension in the string

`\mu` is the linear mass density

In this problem, we have:

`T=2 \cdot 4 N=8 N` (final tension in the rope, which is twice the initial tension)

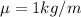`\mu = 1 kg/m` --> mass density of the rope

Substituting into the formula, we find

`v=\sqrt{(8 N)/(1 kg/m)}=2.8 m/s`