Question

A group of people were given a personality test to determine if they were Type A or Type B. The results are shown in the table below:

Answer 1

Option A: P(Male or Type B) > P(Male | Type B)

Explanation:

Total Female = 85 type A, 12 type B ⇒ 97 Female.

Total Male = 65 type A, 38 type B ⇒ 103 Male

Total type A = 65 + 85 = 150

Total type B = 12 + 38 = 50

total number of people = 97 + 103 = 200

Then the probability would be:

P(Male | Type B) =
`(number of male in B)/(total number of male)`

=
`(38)/(103)`

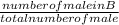
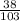
= 0.368

P(Male or Type B) =
`(total number of male + (total number of people in B - total number of male in B))/(total number of male)`

=
`(103 + (50 - 38))/(200)`

=
`(103 + 12)/(200)`

=
`(115)/(200)`

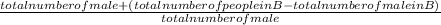
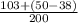
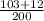
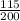
= 0.575

Hence, P(Male or Type B) > P(Male | Type B)