Answer:
1.94
Explanation:
We substitute -4 into as x in the equation, but first what is e?
e is a term that represents the base of a natural logarithm and is a irrational number, its called Euler's number. e is equivalent to:
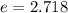
We can substitute -4 into the equation
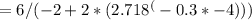

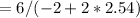
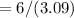
[tex]=1.94
Therefore f(-4)=1.94