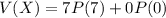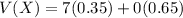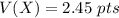Question

if a football team has a 90% chance of making a field goal for three points and 35% chance of making a touchdown for seven point find the expected value of a touchdown

Answer 1

`V(X) = 2.45\ pts`

Explanation:

We look for the expected value for a touchdown.

If X represents the number of points scored per touchdown scored, then X is a discrete random variable, and by definition, the expected value V (X) for a discrete random variable is defined as:

`V(X) = \sum{XP(X)}`

Where P(X) is the probability that X will occur.

In the sample space of the random variable X there are two possible values.

`X = 7` points (1 touchdown) with
`P(7) = 0.35`

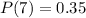
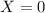`X = 0` points (0 touchdown) with
`P(0) = 1-0.35 = 0.65`

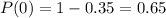
Then the expected value V(X) is:

`V(X) = 7P(7) + 0P(0)`

`V(X) = 7(0.35) + 0(0.65)`

`V(X) = 2.45\ pts`