Answer: Measure of ∠BAM is 30°.
Explanation: As shown in the attached figure, points A and B split the circle with center O into two arcs. Major of the minor arc is 150°. And, the point M splits the major arc in the ratio 2 : 5.
We are to find the measure of ∠BAM.
Since the measure of minor arc AB is 150°, so the measure of major arc AB will be
360° - 150° = 210°.
Also, point M divides the major arc AB in the ratio 2 : 5, so we have
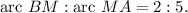
Therefore, the measure of ∠BOM is given by
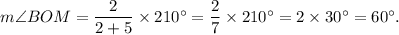
We know that the measure of the angle subtended at the center by an arc is equal to twice the measure of the angle subtended at the circumference by the same arc.
That is, for arc BC, we get
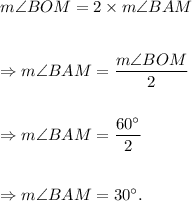
Thus, the measure of ∠BAM is 30°.