Question

The life expectancy of a certain tire is a normal distribution with the mean = 40,000 miles, standard deviation is 1,000 miles. Find the probability that a tire will last more than 39,000 miles.

Answer 1

`P = 84\%`

Explanation:

The average is:

`\mu = 40,000\ miles`

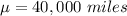
The standard deviation is:

`\sigma = 1,000\ miles`

We want the probability that a tire lasts more than 39,000 miles.

This is:

`P (X>39,000)`

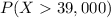
Now we must transform these values to those of a standard normal distribution to facilitate calculation by using the probability tables.

`P (X> 39,000)\\\\P (X-\mu> 39,000-40,000)\\\\P ((X-\mu)/(\sigma)> (39,000 -40,000)/(1,000))\\\\P (Z> -1)`

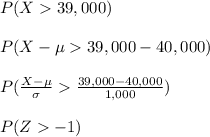
This is:

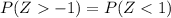`P(Z> -1) = P(Z<1)` ---------- (For the symmetry of the standard normal distribution)

When you search for the normal standard table, you get the following value:

`P(Z <1) = 0.8413\\\\P(Z> -1) = 0.8413`