Question

Brew Ha Ha Coffee produces two types of coffee blends: Morning,x,and House,y. The Morning blend has 9oz of a Guatemalan coffee and 7oz of Brazilian coffee. The company makes $2 in profit from each bag of Morning Blend sold and $2.50 in profit from each bag of House Blend sold. The company has 400oz of both the Guatemalan and Brazilian coffees available.

This set of inequalities represent the constraints in this situation.
9x+6y<400
7x+10y<400
X>0
Y>0

The company wants to maximize its profits by using the objective function P = 2x + 2.5y

What is the maximum profit.

88
0
160
106

Answer 1

Fourth option

Explanation:

When graphing the given inequalities you will get a region like the one shown in the attached image. This region is delimited by 4 straight

`x = 0\\\\y = 0\\\\9x + 6y = 400\\\\7x + 10y = 400`

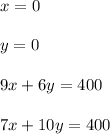
The points indicated at the ends of the region are the maximum possible values of x and y.

We must test these points in the objective function
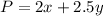`P = 2x + 2.5y` and see which point maximizes the value of P.

Remember that the boundaries of the region are not included.

We can prove the point x = 0 and y = 39 because (0,4) is not included in the region.

`P = 2(0) + 2.5(39) = 97.5`

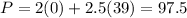
Now we test the point x = 33 and y = 16

`P = 2(33) + 2.5(16) = 106`

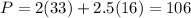
Now we test the point x = 44 and y = 0

`P = 2(44) + 2.5(0) = 88`

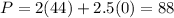
Finally the optimal value is:

x = 33 oz

y = 16 oz

With a gain of $106