Question

Suppose that there are two types of tickets to a show: advance and same-day. The combined cost of one advance ticket and one same-day ticket is $55. For one performance, 20 advance tickets and 35 same-day tickets were sold. The total amount paid for the tickets was $1700. What was the price of each kind of ticket?

Answer 1

Price of advance ticket: 15$

Price of same-day ticket: $40

Explanation:

Let
`y` be the price of one advance ticket and
`x` the cost of one same day ticket.

We know that the combined cost of one advance ticket and one same-day ticket is $55, so

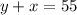`y+x=55` equation (1)

We also know that 20 advance tickets and 35 same-day tickets cost $1700, so

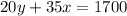`20y+35x=1700` equation (2)

Now, let's solve our system of equations step-by-step:

step 1. Solve for
`x` in equation (1)

`y+x=55`

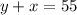
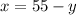`x=55-y` equation (3)

step 2. Replace equation (3) in equation (2)

`20y+35x=1700`

`20y+35(55-y)=1700`

`20y+1925-35y=1700`

`-15y=-225`

`y=(-255)/(-15)`

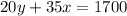
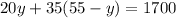
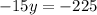
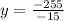
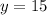`y=15` equation (4)

step 3. Replace equation (4) in equation (3)

`x=55-y`

`x=55-15`

`x=40`

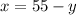
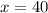
We can conclude that the price of one advance ticket is $15 and the price of one same-day ticket is $40.