Answer: option a.
Explanation:
By definition we know that:
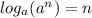
Where a is the base of the logarithm.
We also know that:
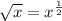
Then you can rewrite the logarithm given in the problem, as you can see below:
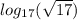
And keeping on mind the property, you obtain:
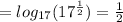
Therefore, you can conclude that the answer is the option a.