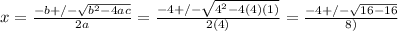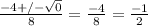Question

The dimensions of a square and equilateral triangle are shown below. If the difference between the area of the square and the perimeter of the triangle is equal to 3, what is a possible value of x?

A. -1/2
B. 1/4
C. 4
D. 8

Answer 1

A

Explanation:

The area of a square is A = s². So the area of this square is A = (2x+2)² = 4x² + 8x + 4.

The perimeter of the triangle is 4/3x + 4/3x+4/3x = 12/3x = 4x.

The difference between the two values is subtraction. Subtract the expressions and simplify.

4x² + 8x + 4 -4x = 4x² + 4x + 4

This expression is also equal to 3. Set it equal to 3 and solve for x.

4x² + 4x + 4 = 3

4x² + 4x + 1 = 0

Substitute a = 4, b = 4 and c = 1 into the quadratic formula.

The quadratic formula is
`x=(-b+/-√(b^2-4ac) )/(2a)`.

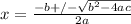Substitute and you'll have:

`x=(-b+/-√(b^2-4ac) )/(2a) =(-4+/-√(4^2-4(4)(1)) )/(2(4))=(-4+/-√(16-16) )/(8))`

`(-4+/-√(0) )/(8) = (-4)/(8)=(-1)/(2)`