Question

Please help, show all work, asappp

Find the slope through the points (12, -18), (11,12)
Find the slope through the points (-18, -20), (-18, -15)
Find the X and Y intercepts: 4x + y = 5
Find the X and Y intercepts: y = 5x - 4
Write the equation of the line with a slope of zero and the point (3,4)?
What is the slope of the line x = 1?

Answer 1

QUESTION 1

We want to find the slope through the points (12,-18), (11,12).

We use the slope formula,

`m = \frac{y_2-y_1} {x _2-x_1}`

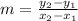
We substitute the points to get,

`m = (12 - - 18)/(11 - 12)`

`m = (30)/( - 1) = - 30`

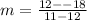
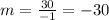
The slope is -30.

QUESTION 2.

We want to find the slope through the points (-18, -20), (-18, -15).

We use the slope formula again to obtain,

`m = ( - 15 - - 20)/( - 18 - - 18)`

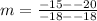
We simplify to get;

`m = (5)/(0)`

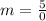
Division by zero means the slope is not defined.

QUESTION 3

The given equation is 4x + y = 5.

At x-intercept, y=0.

We put y=0 into the equation to get,

`4x + 0 = 5`

`4x = 5`

`x = (5)/(4)`

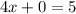
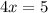
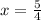
The x-intercept is

`( (5)/(4) , 0)`

To find the y-intercept,we substitute x=0 into the equation to get,

`4(0) + y = 5`

`y = 5`

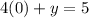
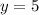
The y-intercept is (0,5)

QUESTION 4.

The given equation is

`y = 5x - 4`

To find the y-intercept put x=0 into the equation.

`y = 5(0) - 4`

`y = - 4`

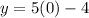
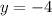
(0,-4)

To find the x-intercept, put y=0,

`0 = 5x - 4`

`4 = 5x`

`(4)/(5) = x`

`( (4)/(5) ,0)`

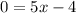
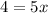
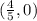
QUESTION 5

To find the equation of a line given the slope m, and a point

`(x_1,y_1)`

we use the formula,

`y-y_1=m(x-x_1)`

The given line has slope zero and passes through

(3,4)

The equation is

`y - 4 = 0(x - 3)`

`y - 4 = 0`

`y = 4`

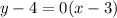
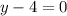
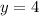
Question 6

The given equation is

`x = 1`

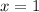
This is the equation of a line that is parallel to the y-axis.

The slope of all lines parallel to the x-axis is undefined.

The slope of x=1 is not defined.