Question

The equation that models the height above or below equilibrium in inches, h, of a spring over time in seconds, t, is h = -15 cos(2pi/5 t). At which times will the spring be at a height of 8 in. above equilibrium? Select two of the following, make two selections.

Answer 1

1.7 seconds, and

3.3 seconds

Explanation:

We simply need to plug in 8 into h and solve for t:

`h=-15Cos((2\pi)/(5)t)\\8=-15Cos((2\pi)/(5)t)\\-(8)/(15)=Cos((2\pi)/(5)t)\\(2\pi)/(5)t=Cos^(-1)(-(8)/(15))\\(2\pi)/(5)t=2.13\\t=(2.13)/((2\pi)/(5))\\t=1.70`

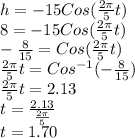
Since cosine is negative in the 3rd quadrant as well, we need to figure out the 3rd quadrant equivalent of 2.13 radians.

First, π - 2.13 radians = 1.01 radians.

Then, we add 1.01 to π radians, so we get 4.15 radians

Solving from the last part, we have:

`t=(4.15)/((2\pi)/(5))\\t=3.3`

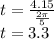
also, t = 3.30 seconds

*Note: we put the calculator mode in radians when solving

So, t = 1.7 seconds & 3.30 seconds