Question

What is the solution to this system of linear equations?

7x - 2y = -6

8x + y = 3

A.(-6,3)
B.(0,3)
C.(1,-5)
D.(15,-1)
​

Answer 1

(0,3)

B is correct

Explanation:

Given: The system of equation.

`7x-2y=-6`

`8x+y=3`

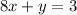
Now, we solve for x and y using elimination method.

Elimination method: In this method to make the coefficient of one variable same and then cancel out by addition of both equation.

Multiply 2nd equation by 2 and we get

`16x+2y=6`

`7x-2y=-6`

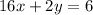
Add both equation and eliminate y

`23x=0`

`x=0`

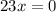
Put x=0 into 1st equation, 7x-2y=-6

7(0) - 2y = -6

y = 3

Solution: x = 0 and y = 3

Hence, The solution of the equation would be (0,3)

Answer 2

B. (0, 3)

Explanation:

Trying the offered solutions in the given equations gets you there pretty quickly.

7·(-6) -2(3) ≠ -6 . . . eliminates choice A

__

7·0 -2·3 = -6

8·0 +3 = 3 . . . . . . . choice B is the solution