Answer:
a) The point (4, 122) represents that the cost of 4 tickets is $122
b) The unit rate is 30.5 dollars per ticket
c) The cost of buying 10 tickets is $305
Explanation:
Let us solve the question
From the given graph
∵ The x-axis represents the number of tickets
∵ The y-axis represents the cost of tickets in dollars
∴ The line represents the relationship between the number of tickets
and their cost
a)
∵ The point (4, 122) lies on the line
∴ x = the number of tickets
∴ y = their cost
∵ x = 4 and y = 122
∴ The cost of the 4 tickets is 122 dollars
∴ The point (4, 122) represents that the cost of 4 tickets is $122
b)
∵ The unit rate is the slope of the line
∵ The slope of the line = Δy/Δx, where
- Δy = y2 - y1
- Δx = x2 - x1
∵ The line passes through points (0, 0) and (2, 61)
∴ x1 = 0 and x2 = 2
∴ y1 = 0 and y2 = 61
→ Substitute them in the rule of the slope above
∴ The slope of the line =
=
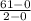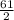= 30.5
∴ The unit rate is 30.5 dollars per ticket
c)
∵ The linear equation is y = m x + b, where
- m is the slope of the line
- b is the y-intercept (value y at x = 0)
∵ m = 30.5 ⇒ the slope of the lone
∵ b = 0 ⇒ The line passes through the origin point (0, 0)
∴ The equation of the line is y = 30.5x
∵ x = 10 ⇒ number of tickets
→ Substitute x by 10 in the equation to find the cost of 10 tickets
∴ y = 30.5(10)
∴ y = 305
∴ The cost of buying 10 tickets is $305