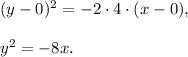Question

Find the standard form of the equation of the parabola with a focus at (-2, 0) and a directrix at x = 2.

Answer 1

`y^2=-8x`

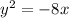
Explanation:

The directrix intersects the x-axis at point (2,0). Points (-2,0) and (2,0) are symmetric about the origin, so the vertex of the parabola is placed at the origin (0,0).

The parameter p of the parabola is the distance from the focus to the directrix, thus p=4.

The branches of the parabola go in negative direction of x-axis, because the focus lies to the left from the vertex.

The equation of the parabola is

`(y-0)^2=-2\cdot 4\cdot (x-0),\\ \\y^2=-8x.`