A simple way to see what was done is to add and subtract -1 from the numerator:

(provided that
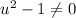 , or
, or
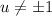 )
)
###
Suppose you had a slightly more complex integrand, like
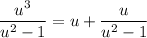
How do we know that? (Assume we don't already know the previous result, so that it's not just a matter of multiplying both sides by
 .) Simple polynomial division:
.) Simple polynomial division:
 , and
, and
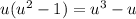 . Subtracting this from
. Subtracting this from
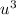 gives a remainder of
gives a remainder of
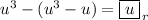 , so
, so

(where
 and
and
 denote "quotient" and "remainder")
denote "quotient" and "remainder")