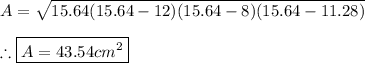Question

Need help ASAP

What is the area of this triangle
Enter your answer as a decimal in the box

Answer 1

`\boxed{A=43.54cm^2}`

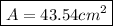
Explanation:

To find this area we will use the law of cosine and the Heron's formula. First of all, let't find the unknown side using the law of cosine:

`x^2=12^2+8^2-2(12)(8)cos(65^(\circ)) \\ \\ x^2=144+64-192(0.42) \\ \\ x^2=208-80.64 \\ \\ x^2=127.36 \\ \\ x=√(127.36) \\ \\ \therefore \boxed{x=11.28cm}`

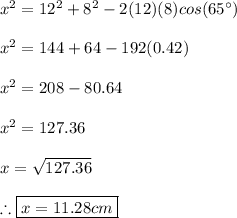
Heron's formula (also called hero's formula) is used to find the area of a triangle using the triangle's side lengths and the semiperimeter. A polygon's semiperimeter s is half its perimeter. So the area of a triangle can be found by:

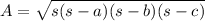`A=√(s(s-a)(s-b)(s-c))` being
`a,\:b\:and\:c` the corresponding sides of the triangle.

So the semiperimeter is:

`s=(12+8+11.28)/(2) \\ \\ s=15.64cm`

So the area is:

`A=√(15.64(15.64-12)(15.64-8)(15.64-11.28)) \\ \\ \therefore \boxed{A=43.54cm^2}`