Question

The following equation describes a circle.

2x^2 - 20x + 2y^2 + 8y =40
What are the center and radius of the circle?

Answer 1

Based on the given equation of the circle, the center of the circle is (5, -2), and the radius is 7.

How to determine the center and radius of the circle

To determine the center and radius of the circle described by the equation rewrite the equation in the standard form of a circle equation, which is

`(x - h)^2 + (y - k)^2 = r^2.`

First, complete the square for both the x and y terms:

`2x^2 - 20x + 2y^2 + 8y = 40`

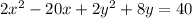
To complete the square for the x-terms, factor out a 2 from the
`x^2` and x terms:

`2(x^2 - 10x) + 2y^2 + 8y = 40`

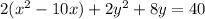
Now, add and subtract the square of half the coefficient of x, which is
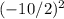`(-10/2)^2` = 25:

`2(x^2 - 10x + 25 - 25) + 2y^2 + 8y = 40`

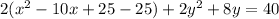
Simplifying inside the parentheses:

`2((x - 5)^2 - 25) + 2y^2 + 8y = 40`

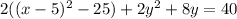
Similarly, for the y-terms, add and subtract the square of half the coefficient of y, which is

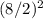`(8/2)^2` = 16:

`2((x - 5)^2 - 25) + 2(y^2 + 4y + 4 - 4) = 40`

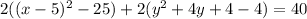
Simplifying inside the parentheses:

Now, let's distribute the 2 on both terms:

`2(x - 5)^2 - 50 + 2(y + 2)^2 - 8 = 40\\2(x - 5)^2 + 2(y + 2)^2 - 58 = 40`

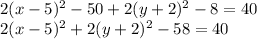
Rearrange the equation:

`2(x - 5)^2 + 2(y + 2)^2 = 98`

Divide both sides by 2 to simplify:

`(x - 5)^2 + (y + 2)^2 = 49`

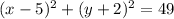
Now the equation is in the standard form of a circle equation.

Comparing it to
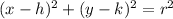`(x - h)^2 + (y - k)^2 = r^2`, we can see that the center of the circle is (h, k) = (5, -2), and the radius squared is r^2 = 49.

Take the square root of both sides

r = 7.

Therefore, the center of the circle is (5, -2), and the radius is 7.

Answer 2

Center = (5, -2) and radius = √33

Explanation:

The equation of a circle is given by the formula;

(x-a)² + (y-b)² = r² ; where (a,b) is the center of the circle and r is the radius of the circle.

In this case;

2x² - 20x + 2y² + 8y =40 ;

Dividing both sides of the equation by 2 we get;

x² - 10x + y² + 4y = 20

we can then use the completing the square on both x and y terms.

x² - 10x + y² + 4y = 20

x² + 2(-5)x + 25 + y² + 2(2) y + 4 = 20 +9 + 4

In standard form we get;

(x-5)² + (y+2)² = 33

Therefore;

Center = (5, -2) and radius = √33