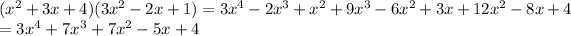Question

Multiply (x^2+3x+4)(3x^2-2x+1)

Answer 1

B

Explanation:

When multiplying
`(x^2+3x+4)(3x^2-2x+1)`, we can use the distributive property of multiplication over addition:

`(x^2+3x+4)(3x^2-2x+1)=x^2\cdot 3x^2+x^2\cdot (-2x)+x^2\cdot 1+3x\cdot 3x^2+3x\cdot (-2x)+3x\cdot 1+4\cdot 3x^2+4\cdot (-2x)+4\cdot 1=3x^4-2x^3+x^2+9x^3-6x^2+3x+12x^2-8x+4.`

Now group the like terms:

`3x^4-2x^3+x^2+9x^3-6x^2+3x+12x^2-8x+4=3x^4+(-2x^3+9x^3)+(x^2-6x^2+12x^2)+(3x-8x)+4=3x^4+7x^3+7x^2-5x+4.`

Answer 2

Answer: option B

Explanation:

To solve this exercise you must apply the proccedure shown below:

- Apply the Distributive property (Remember that when you multiply two powers with the same base, you must add the exponents).

`b^m*b^n=b^((m+n))`

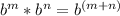
- Add the like terms.

Therefore, you obtain that the product is:

`(x^2+3x+4)(3x^2-2x+1)=3x^4-2x^3+x^2+9x^3-6x^2+3x+12x^2-8x+4\\=3x^4+7x^3+7x^2-5x+4`