Answer:
The answer are options
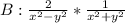 and
and
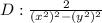
Explanation:
As all the options are multiplication of fractions the option A cannot be an answer because the numerator multiplication is 1 and different to 2. In the case of option C, observe that if we multiply the denominators we have:
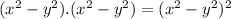
As we know for the expanding of the square binomials:

Which is different from the denominator compared:
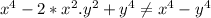
Thus option B cannot be an answer either.
Noting that the denominator compared is a square of two difference by definition, therefore, can be written as:
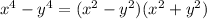
This results in the same denominator as option B. So, option B is a possible answer.
Finally, in the denominator of option D, we can solve the exponents of this factor.
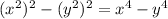
Which results in the same as the denominator compared, this let option D to be a possible answer.