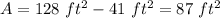Answer:
Part a) The area of the shaded region is
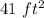
Part b) The area of the nonshaded region is
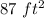
Explanation:
we know that
The total area is equal to the area of the shaded region plus the area of the nonshaded region
step 1
Find the total area
The total area is equal to the area of the rectangle
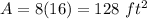
step 2
Find the area of the shaded region
The area of the shaded region is equal to the area of the trapezoid minus the area of the smaller square
so
 -2^(2) \\ \\A=(1)/(2)[9](10) -4\\ \\A=41\ ft^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/nkmreg54vs78mtmeb8jd7ss8tu8u0h88e8.png)
step 3
Find the area of the nonshaded region
The area of the nonshaded region is equal to the total area minus the area of the shaded region
so