Answer:
a. 3u + 2v
Explanation:
To solve this problem, we need to apply some properties of logarithms. Properties are useful to simplify complicated expressions. Here we need to use a very useful property of logarithms called the logarithm of a product is the sum of the logarithms, that is:
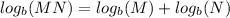
From the function, it is then true that:
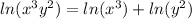
The other property we must use is Logarithm of a Power:

Then:
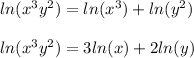
Since:
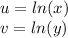
Then:
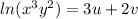
Finally, the correct option is:
a. 3u + 2v