Question

Evaluate the logarithm. ln=1/√e^3

Answer 1

b.
`-(3)/(2)`

Explanation:

The given logarithm is

`\ln((1)/(√(e^3) ) )`

Use the quotient rule of logarithm;
`\ln((a)/(b))=\ln(a)-\ln(b)`

`=\ln(1)-\ln(√(e^3))`

`=\ln(1)-\ln(e^{(3)/(2)})`

Use the power rule;
`\ln(a^n)=n\ln(a)`

`=\ln(1)-(3)/(2)\ln(e)`

Recall that logarithm of 1 is zero and also logarithm of the base is 1.

`=0-(3)/(2)(1)`

`=-(3)/(2)`

Answer 2

option b

-3/2

Explanation:

Given in the question an expression

ln
`(1)/(√(e^3) )`

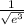
First apply logarithm divide rule

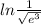`ln(1)/(√(e^3) )` = ln1 - ln√e³

ln(1) = 0

so

ln1 - ln√e³ = 0 - ln√e³

-ln√e³ = -ln(e³)^1/2

Apply logarithm power rule

- ln(e³)^1/2 = -lne
`^(3)/(2)`

-3/2ln(e)

As we know that

ln(e) = 1

so,

-3/2(1)

-3/2