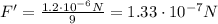Question

two charges attract each other with a force of 1.2 * 10⁻⁶N. Calculate the force that would act between the two charges when distance is doubled, halved, trebled.

Answer 1

1. When the distance is doubled:
`3\cdot 10^(-7)N`

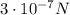
The electrostatic force between two charges is given by:

`F=k(q_1 q_2)/(r^2)`

where

k is the Coulomb's constant

q1 and q2 are the two charges

r is the distance between the two charges

The initial force between the two charges is
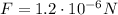`F=1.2\cdot 10^(-6)N`. In this part of the problem, the distance between the two charges is doubled, so we can write

`r'=2r`

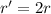
And substituting into the formula, we find the new force:

`F'=k(q_1 q_2)/(r'^2)=k(q_1 q_2)/((2r)^2)=(1)/(4)k(q_1 q_2)/(r^2)=(F)/(4)`

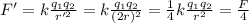
So, the force is reduced to 1/4 of its original value. Therefore, it is

`F'=(1.2\cdot 10^(-6) N)/(4)=3\cdot 10^(-7)N`

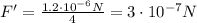
2. When the distance is halved:
`4.8\cdot 10^(-6)N`

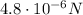
The initial force between the two charges is
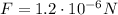`F=1.2\cdot 10^(-6)N`. In this part of the problem, the distance between the two charges is halved, so we can write

`r'=r/2`

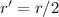
And substituting into the formula, we find the new force:

`F'=k(q_1 q_2)/(r'^2)=k(q_1 q_2)/((r/2)^2)=4k(q_1 q_2)/(r^2)=4F`

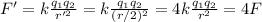
So, the force is quadrupled. Therefore, it is

`F'=4(1.2\cdot 10^(-6) N)=4.8\cdot 10^(-6)N`

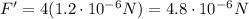
3. When the distance is tripled:
`1.33\cdot 10^(-7)N`

The initial force between the two charges is
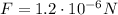`F=1.2\cdot 10^(-6)N`. In this part of the problem, the distance between the two charges is tripled, so we can write

`r'=3r`

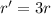
And substituting into the formula, we find the new force:

`F'=k(q_1 q_2)/(r'^2)=k(q_1 q_2)/((3r)^2)=(1)/(9)k(q_1 q_2)/(r^2)=(F)/(9)`

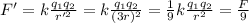
So, the force is reduced to 1/9 of its original value. Therefore, it is

`F'=(1.2\cdot 10^(-6) N)/(9)=1.33\cdot 10^(-7)N`