QUESTION 1
Recall the mnemonics; SOH
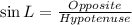
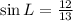
QUESTION 2
Recall the mnemonics; CAH
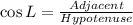
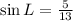
QUESTION 3
Recall the mnemonics; TOA
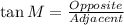
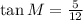
QUESTION 4
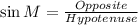
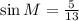
QUESTION 5
a) From the Pythagoras Theorem,
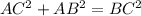
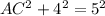
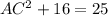
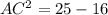
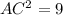
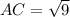
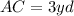
b) Using the cosine ratio,
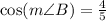
Take the inverse cosine of both sides;
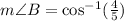
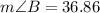
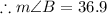 to the nearest tenth.
to the nearest tenth.
c)
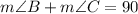
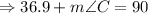
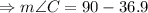
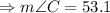
QUESTION 6
a) using the sine ratio,
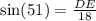
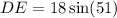
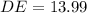
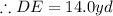 to the nearest tenth.
to the nearest tenth.
b) Using the cosine ratio,
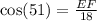
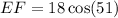
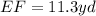 to the nearest tenth.
to the nearest tenth.
c)
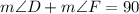
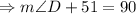
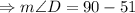
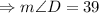
QUESTION 7
a) Using the Pythagoras Theorem;
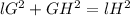
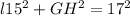
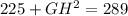
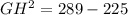
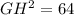
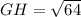
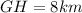
b) Using the sine ratio,
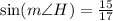
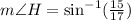
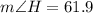
c)
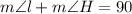
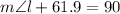
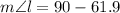
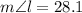
QUESTION 8
We plot the points as shown in the diagram.
QUESTION 9
From the diagram, the side lengths XY and YZ can be obtained by counting the boxes. Each box is 1 unit.
This implies that;
XY =3 units
YZ=5 units.
We use Pythagoras Theorem, to obtain XZ.
This implies that;
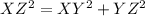
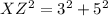
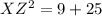
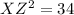
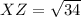 units
units
QUESTION 10.
a) Using the tangent ratio;
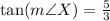
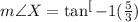
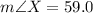
b)
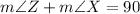
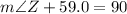
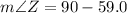
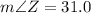
QUESTION 11
a) Triangle BCD is shown in the attachment.
The length of side DC=|3-2|=1 unit
The length of side DB=|4-3|=1 unit
Using Pythagoras Theorem;
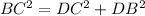
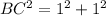
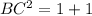
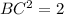
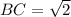
b) DB is perpendicular to DC, therefore m<D=90 degrees.
The length of DB is equal the length of DC.
This implies that;
m<C=m<B=45 degrees.
QUESTION 12
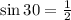
QUESTION 13
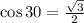
QUESTION 14
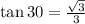
QUESTION 15
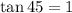
QUESTION 16
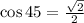
QUESTION 17
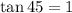
Check attachment for the rest