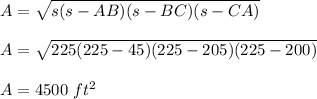Question

The perimeter of Δ ABC is 450 ft. If AB= 9x, BC=41x and CA=40x, what is the area of the triangle?

Answer 1

`A = 4500 ft^2`

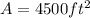
Explanation:

By definition:

The pre-meter P of a triangle ABC is equal to the sum of the length of its sides.

We know that:

`P = 450\ ft\\AB = 9x\\BC = 41x\\CA = 40x`

The perimeter is:

`P = AB + BC + CA\\P = 450 = 9x + 41x + 40x\\90x = 450\\x = 5`

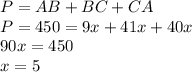
Now we find the length of the sides:

`AB = 45\\BC = 205\\CA = 200`

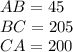
Once the length of the sides is known, we use Heron's formula to calculate the area.

First I find the semiperimeter S.

`S = 0.5(45 + 205 +200)\\S = 225`

Then the Area is:

`A = √(s(s-AB)(s-BC)(s-CA))\\\\A = √(225(225-45)(225-205)(225-200))\\\\A = 4500\ ft^2`