PLS HELP!! A circle is centered at point (-7,-1) and passes through the point (8,7). The radius of the circle is ___ units. The point (-15,_) lies on this circle.

Question

asked Jun 10, 2020 194k views

2 Answers

Serg Tomcat · Answer 1 · 2020-06-14T05:10:54+0000

Answer:

Part 1) The radius of the circle is
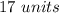
$17\ units$

Part 2) The points (15,14) and (-15,-16) lies on this circle

Explanation:

Part 1

we know that

The distance between the center of the circle at point (-7,-1) and the point (8,7) is equal to the radius of the circle

so

the formula to calculate the distance between two points is equal to

$d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}$

substitute the values

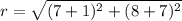
$r=\sqrt{(7+1)^(2)+(8+7)^(2)}$

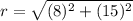
$r=\sqrt{(8)^(2)+(15)^(2)}$

r=√(289)}

$r=17\ units$

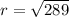
Part 2

we know that

If the point (-15,y) lies on the circle, then the ordered pair must be satisfy the equation of the circle

The equation of the circle is equal to

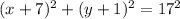(x+7)^(2)+(y+1)^(2)=17^(2) -----> equation of the circle in center radius form

substitute the value of x=-15 in the equation and solve for y

(-15+7)^(2)+(y+1)^(2)=289

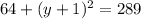
64+(y+1)^(2)=289

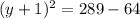
(y+1)^(2)=289-64

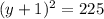
(y+1)^(2)=225

y+1=(+/-)15

y=-1(+/-)15

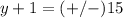
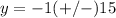
so

y=14

y=-16

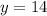
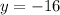
therefore

The points (15,14) and (-15,-16) lies on this circle

see the attached figure to better understand the problem