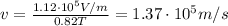Question

A uniform electric field of magnitude 112 kV/m is directed upward in a region of space. A uniform magnetic field of magnitude 0.82 T perpendicular to the electric field also exists in this region. A beam of positively charged particles travels into the region. Determine the speed of the particles at which they will not be deflected by the crossed electric and magnetic fields. (Assume the beam of particles travels perpendicularly to both fields.)

Answer 1

`1.37\cdot 10^5 m/s`

Step-by-step explanation:

The beam of positively charged particles would not be deflected if the electric force acting on them is equal to the magnetic force:

`F_E = F_B\\qE = qvB sin \theta`

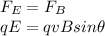
where

q is the charge of the particles

E is the magnitude of the electric field

v is the speed of the particles

B is the intensity of the magnetic field

`\theta` is the angle between the direction of v and B

Since the beam of particles travels perpendicular to the magnetic field, we have
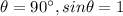`\theta=90^(\circ), sin \theta=1`. So, we can rewrite the equation as

`v=(E)/(B)`

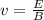
where

`E=112 kV/m = 1.12\cdot 10^5 V/m\\B=0.82 T`

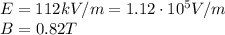
Substituting into the formula,

`v=(1.12\cdot 10^5 V/m)/(0.82 T)=1.37\cdot 10^5 m/s`