Question

Solve a triangle with a=25, b=30, and C= 160°
(picture provided)

Answer 1

Option d.

Explanation:

For this problem we have 2 sides of a triangle (a and b) and the angle between them C = 160 °.

We have a triangle of type SAS.

We have:

a=25

b=30

C= 160°

Then we use the law of cosine.

`c = \sqrt{a^2 +b^2 - 2abcos(C)`

Now we substitute the values in the formula to find c

`c = √(25^2 +30^2 - 2(25)(30)cos(160\°))\\\\c = 54.2`

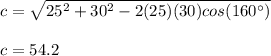
Now we use the cosine theorem to find B. (You can also use the sine)

`b = √(a^2 +c^2 - 2accos(B))\\\\b^ 2 = a^2 +c^2 - 2accos(B)\\\\b^ 2 -a^2 -c^2 =- 2accos(B)\\\\(a^2 +c^2 -b^2)/(2ac) =cos(B)\\\\B = arcos((a^2 +c^2 -b^2)/(2ac))\\\\B = arcos((25^2 +54.2^2 -30^2)/(2(25)(54.2)))\\\\B = 10.9\°`

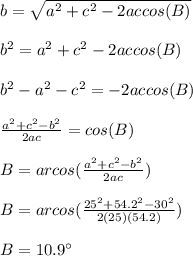
Finally:

`A=180\° - B- C\\\\A = 180\° - 10.9\° - 160\°\\\\A = 9.1\°`