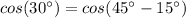Answer:
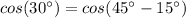
Explanation:
To solve this problem you must know the formula of subtraction of angles for the function cosx.
The formula is:
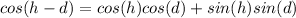
We can write 30° as: 45° - 15°
Then:
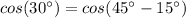
Using the formula for subtraction of angles we have:
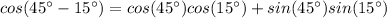
Notice that we have achieved the expression shown in the statement
Finally: