Question

What kind of symmetry is displayed by the graph of catenary y=e^x+e^-x/2

Answer 1

b

Explanation:

Answer 2

Option b

Explanation:

To solve this problem we must test if the function is even.

If f(-x) = f(x) then the function is even and is symmetric with respect to the y-axis.

If f(-x) = -f(x) then the function is odd and has symmetry with respect to the origin.

We have the function:

`f(x) = (e^x + e^(-x))/(2)`

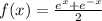
We make:

`f(-x) = (e^(-x) + e^(-(-x)))/(2)`

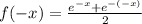
Rewriting the function we have

`f(-x) = (e^(-x) + e^(x))/(2) = (e^(x) + e^(-x))/(2)\\\\f(-x) = f(x)`

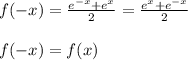
Finally, the function has symmetry with respect to the y axis.