Question

(a) Use differentiation to find a power series representation forf(x) =1(6 + x)2.f(x) =∞ leftparen1.gif(−1)n(n+1)xn6n+2​ rightparen1.gifsum.gifn = 0What is the radius of convergence, R?R = (b) Use part (a) to find a power series forf(x) =1(6 + x)3.f(x) =∞ leftparen1.gif(−1)n(n+3)(n+1)xn6n+5​ rightparen1.gifsum.gifn = 0What is the radius of convergence, R?R = (c) Use part (b) to find a power series forf(x) =x2(6 + x)3.f(x) =∞ leftparen1.gif(−1)n(n+2)(n+1)xn+26n+3​ rightparen1.gifsum.gifn = 2What is the radius of convergence, R?R =

Answer 1

(a) Wild guess:

Recall the power series

`\displaystyle\frac1{1-x}=\sum_(n=0)^\infty x^n`

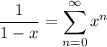
With some manipulation, we can write

`\displaystyle\frac1{6+x}=\frac16\frac1{1-\left(-\frac x6\right)}=\frac16\sum_(n=0)^\infty\left(-\frac x6\right)^n=\sum_(n=0)^\infty((-x)^n)/(6^(n+1))`

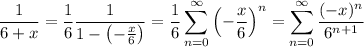
Take the derivative and we get

`\displaystyle-\frac1{(6+x)^2}=-\sum_(n=0)^\infty(n(-x)^(n-1))/(6^(n+1))`

`\displaystyle=-\sum_(n=1)^\infty(n(-x)^(n-1))/(6^(n+1))`

`\displaystyle=-\sum_(n=0)^\infty((n+1)(-x)^n)/(6^(n+2))`

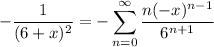
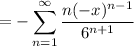
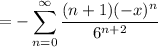
so we have

`\displaystyle\frac1{(6+x)^2}=\sum_(n=0)^\infty((n+1)(-x)^n)/(6^(n+2))`

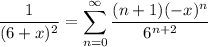
By the ratio test, this series converges if

`\displaystyle\lim_(n\to\infty)\left|(((n+2)(-x)^(n+1))/(6^(n+3)))/(((n+1)(-x)^n)/(6^(n+2)))\right|=\left|\frac x6\right|\lim_(n\to\infty)(n+2)/(n+1)=\left|\frac x6\right|<1`

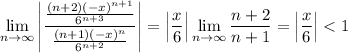
or
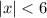`|x|<6`, so that the radius of convergence is
`R=6`.

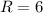(b). If we take the second derivative, we get

`\displaystyle\frac2{(6+x)^3}=\sum_(n=0)^\infty(n(n+1)(-x)^(n-1))/(6^(n+2))`

`\displaystyle=\sum_(n=1)^\infty(n(n+1)(-x)^(n-1))/(6^(n+2))`

`\displaystyle=\sum_(n=0)^\infty((n+1)(n+2)(-x)^n)/(6^(n+3))`

`\displaystyle\frac1{(6+x)^3}=\frac12\sum_(n=0)^\infty((n+1)(n+2)(-x)^n)/(6^(n+3))`

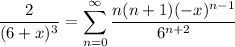
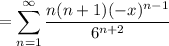
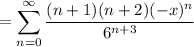
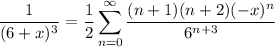
Apply the ratio test again and we get
`R=6`.

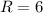(c) Multiply the previous series by
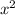`x^2` and we get

`\displaystyle(x^2)/((6+x)^3)=\frac12\sum_(n=0)^\infty((n+1)(n+2)(-x)^nx^2)/(6^(n+3))`

`\displaystyle=\frac12\sum_(n=0)^\infty((n+1)(n+2)(-1)^nx^(n+2))/(6^(n+3))`

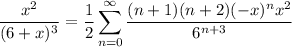
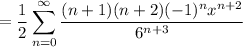
The ratio test yet again tells us
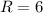`R=6`.