Answer:
The rectangular prism has the greatest surface area
Explanation:
Verify the surface area of each container
case A) A cone
The surface area of a cone is equal to
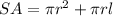
we have
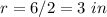 ----> the radius is half the diameter
----> the radius is half the diameter
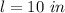
substitute the values
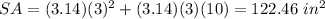
case B) A cylinder
The surface area of a cylinder is equal to
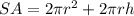
we have
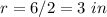 ----> the radius is half the diameter
----> the radius is half the diameter

substitute the values
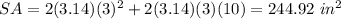
case C) A square pyramid
The surface area of a square pyramid is equal to
![SA=b^(2) +4[(1)/(2)bh]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/bgl8okfeavupb7c1v7k9q2kvqdbwbssewo.png)
we have
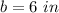 ----> the length side of the square
----> the length side of the square
 ----> the height of the triangular face
----> the height of the triangular face
substitute the values
![SA=6^(2) +4[(1)/(2)(6)(10)]=156\ in^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/g7xr7c8rexbkufcwurx3ql20mgy5kn3qrw.png)
case D) A rectangular prism
The surface area of a rectangular prism is equal to
![SA=2b^(2) +4[bh]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x3h240g42k47xt89oc128cr5tlzytac2xa.png)
we have
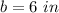 ----> the length side of the square base
----> the length side of the square base
 ----> the height of the rectangular face
----> the height of the rectangular face
substitute the values
![SA=2(6)^(2) +4[(6)(10)]=312\ in^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1li9a8dw62li0xijwy4mneu72mdz6rb9d0.png)