Answer:
C
Explanation:
In translating graphs of functions, we can follow 2 rules:
1. The graph of
 is the graph of
is the graph of
 shifted a units UP VERTICALLY and the graph of
shifted a units UP VERTICALLY and the graph of
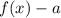 is the graph of
is the graph of
 shifted a units DOWN VERTICALLY.
shifted a units DOWN VERTICALLY.
2. The graph of
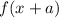 is the graph of
is the graph of
 shifted a units to the LEFT HORIZONTALLY and the graph of
shifted a units to the LEFT HORIZONTALLY and the graph of
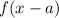 is the graph of
is the graph of
 shifted a units RIGHT HORIZONTALLY.
shifted a units RIGHT HORIZONTALLY.
If we understand the 2 rules above, we clearly know that f(x+2) will be a horizontal shift to the LEFT, of course, with respect to the function
 . Looking at the answer choices, C is right.
. Looking at the answer choices, C is right.