Answer:
Part 1: Find (f/g)(4) = 3
Part 2: Find (f+g)(4) = 28
Explanation:
Part 1: Find (f/g)(4):
(f/g)(4) means divide f function by g function and simplify it. Then plug in 4 into x of that simplified function.
Let's do this:
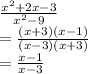
Plugging in 4 into x gives us:
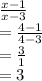
The answer is 3
Part 2: Find (f+g)(4):
(f+g)(4) means add f function and g function and simplify it. Then plug in 4 into x of that simplified function.
Let's do this:
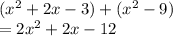
Plugging in 4 into x gives us:
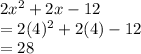
The answer is 28