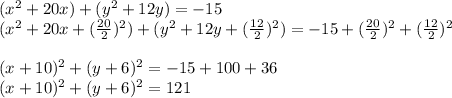Question

the equation of a circle in general form is x squared + y squared + 20x + 12 y + 15 equals 0what is the equation of the circle in standard form ​

Answer 1

Answer:
`(x+10)^2+(y+6)^2=121`

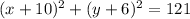
Explanation:

The equation of a circle in the general form is:

`ax^(2)+by^2+cx+dy+e=0`

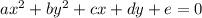
The equaton of a circle in standard form is:

`(x-h)^2+(y-k)^2=r^2`

Where the center is at (h, k) and r is the radius

To write the equation of a circle from general form to standard form, you must complete the squaare, as you can see below:

1- Given the equation in general form:

`x^(2)+y^2+20x+12y+15=0`

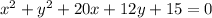
2- Complete the square:

-Group the like terms and move the constant to the other side.

- Complete the square on the left side of the equation.

- Add the same value to the other side.

Then you obtain:

`(x^(2)+20x)+(y^2+12y)=-15\\(x^2+20x+((20)/(2))^2)+(y^2+12y+((12)/(2))^2)=-15+((20)/(2))^2+((12)/(2))^2\\\\(x+10)^2+(y+6)^2=-15+100+36\\(x+10)^2+(y+6)^2=121`