Answer:
The expression which is a polynomial is:
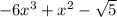
Explanation:
A polynomial expression is a expression of the form:
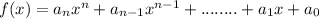
where n belong to non-negative integers and
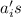 are real numbers.
are real numbers.
1)
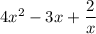
This is not a polynomial because the third term:
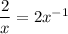 has a negative poswer of x which violates the definition of polynomial.
has a negative poswer of x which violates the definition of polynomial.
2)
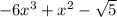
In this each of the term satisfy the definition of polynomial and hence the expression is a polynomial expression.
3)
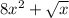
Here the second term is not a integer power and hence violate the definition of polynomial.
4)
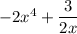
which could also be written as:

Here the second term contain a negative power of x and hence is not a polynomial.