Question

Of 750 people surveyed, 330 were male and 640 had cell phones. Of those with cell phones, 390 were female. What is the probability that a person surveyed was either male or had a cell phone?

a) 360/750 ≈ 0.48
b) 580/750 ≈ 0.7733
c) 700/750 ≈ 0.9333
d) 720/750 ≈ 0.96

Answer 1

HOPE THIS HELPS the answer is B

Answer 2

Option d - 720/750 ≈ 0.96

Explanation:

Given : Of 750 people surveyed, 330 were male and 640 had cell phones. Of those with cell phones, 390 were female.

To find : What is the probability that a person surveyed was either male or had a cell phone?

Solution :

Let M be the number of males i.e. M=330

Let C be the number of cell phones i.e C=640

Total number of people = 750

Of 750 people surveyed, 330 were male

The probability of male is

`P(M)=(330)/(750)`

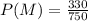
Of 750 people surveyed, 640 had cell phones

The probability of cell phones is

`P(C)=(640)/(750)`

Of those with cell phones, 390 were female.

i.e. reaming were male so 640-390=250

So, Probability of male and cell phone is

`P(M\cap C)=(250)/(750)`

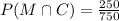
We have to find, the probability that a person surveyed was either male or had a cell phone i.e.
`P(M\cup C)`

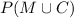
Using formula,

`P(M\cup C)=P(M)+P(C)-P(M\cap C)`

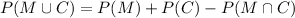
Substitute the values,

`P(M\cup C)=(330)/(750)+(640)/(750)-(250)/(750)`

`P(M\cup C)=(330+640-250)/(750)`

`P(M\cup C)=(720)/(750)`

`P(M\cup C)=0.96`

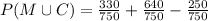
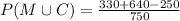
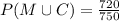
Therefore, Option d is correct.