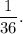Question

A six-sided number cube is rolled

What is the probability of getting a 2 and then a 1, given that the first number rolled was 2?

Answer 1

Answer: The required probability is
`(1)/(36).`

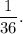
Step-by-step explanation: We are given that a six-sided number cube is rolled.

We are to find the probability of getting a 2 and then a 1, given that the first number rolled was 2.

Let S denotes the sample space of rolling a six-sided cube, A be the event of rolling a 2 and B be the event of rolling a 1.

Then,

n(S) = 6, n(A) = 1 and n(B) = 1.

Now, the probabilities of events A and B :

`P(A)=(n(A))/(n(S))=(1)/(6),\\\\\\P(B)=(n(B))/(n(S))=(1)/(6).`

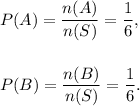
Since the two events A and B are independent of each other, so the required probability is given by

`P(A\cap B)=P(A)* P(B)=(1)/(6)*(1)/(6)=(1)/(36).`

Thus, the required probability is
`(1)/(36).`

Answer 2

♫ - - - - - - - - - - - - - - - ~Hello There!~ - - - - - - - - - - - - - - - ♫

➷There is a dice and you have 6 numbers

The probability is 1/36, since it is 1/6 to get a 2 the first time, and 1/6 to get a 1 the next time.

✽

➶ Hope This Helps You!

➶ Good Luck (:

➶ Have A Great Day ^-^

DOGE