Question

You are given three pieces of wire that have different shapes (dimensions). You connect each piece of wire separately to a battery. The first piece has a length L and cross-sectional area A. The second is twice as long as the first, but has the same thickness. The third is the same length as the first, but has twice the cross-sectional area. Rank the wires in order of which carries the most current (has the lowest resistance) when connected to batteries with the same voltage difference. Rank the wires from most current (least resistance) to least current (most resistance).

Answer 1

`R_3 < R_1 < R_2`

Step-by-step explanation:

The resistance of a wire is given by:

`R=(\rho L)/(A)`

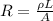
where

`\rho` is the resistivity of the material

L is the length of the wire

A is the cross-sectional area of the wire

1) The first wire has length L and cross-sectional area A. So, its resistance is:

`R_1=(\rho L)/(A)`

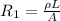
2) The second wire has length twice the first one: 2L, and same thickness, A. So its resistance is

`R_2=(2\rho L)/(A)`

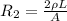
3) The third wire has length L (as the first one), but twice cross sectional area, 2A. So, its resistance is

`R_3=(\rho L)/(2A)`

By comparing the three expressions, we find

`R_3 < R_1 < R_2`

So, this is the ranking of the wire from most current (least resistance) to least current (most resistance).