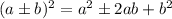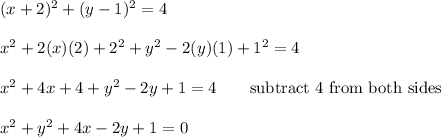Question

what is the general form of the equation of a circle with its Center at -2 1 and passing through -4 one​

Answer 1

`\large\boxed{x^2+y^2+4x-2y+1=0}`

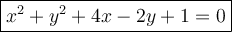
Explanation:

The standard form of an equation of a circle:

`(x-h)^2+(y-k)^2=r^2`

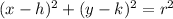
(h, k) - center

r - radius

The general form of an equation of a circle:

`x^2+y^2+Dx+Ey+F=0`

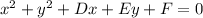
We have the center (-2, 1). Substitute to the equation in the standard form:

`(x-(-2))^2+(y-1)^2=r^2\\\\(x+2)^2+(y-1)^2=r^2`

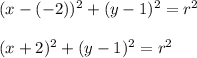
Put thr coordinates of the point (-4, 1) to the equation and calculate a radius:

`(-4+2)^2+(1-1)^2=r^2\\\\r^2=(-2)^2+0^2\\\\r^2=4`

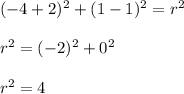
Therefore we have the equation:

`(x+2)^2+(y-1)^2=4`

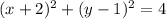
Convert to the general form.

Use
`(a\pm b)^2=a^2\pm 2ab+b^2`

`(x+2)^2+(y-1)^2=4\\\\x^2+2(x)(2)+2^2+y^2-2(y)(1)+1^2=4\\\\x^2+4x+4+y^2-2y+1=4\qquad\text{subtract 4 from both sides}\\\\x^2+y^2+4x-2y+1=0`