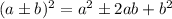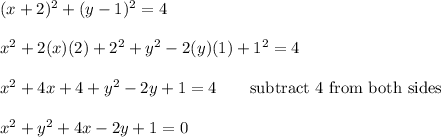Answer:
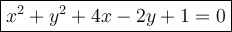
Explanation:
The standard form of an equation of a circle:

(h, k) - center
r - radius
The general form of an equation of a circle:
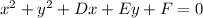
We have the center (-2, 1). Substitute to the equation in the standard form:
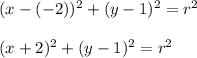
Put thr coordinates of the point (-4, 1) to the equation and calculate a radius:
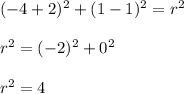
Therefore we have the equation:
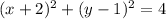
Convert to the general form.
Use