Question

What is the approximate area of the shaded region?

Answer 1

At = 21.5 cm2

Explanation:

At = Asqr - Acircle

At = A1 - A2

A1 = 10^2 = 100

A2 = Pi*(5)^2 = 78.5

At = 100 - 78.5

At = 21.5 cm2

Best regards

Answer 2

For this case we have that by definition:

The area of a circle is:
`A_ {c} = \pi * r ^ 2`

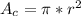
Where r is the radius of the circle.

The area of a square is:
`A_ {s} = l ^ 2`

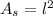
Where l is the side of the square.

The area of the shaded region will be:

`A_ {sr} = A {s} -A_ {c}`

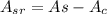
So:

`A_ {s} = 10 * 10\\A_ {s} = 100 \ cm ^ 2`

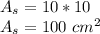
On the other hand:

`A_ {c} = \pi * (\frac {10} {2}) ^ 2\\A_ {c} = \pi * 25\\A_ {c} = 78.5375cm ^ 2`

Finally:

`A_ {sr} = 100-78.5375\\A_ {sr} = 21.4625`

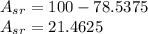
Rounding out, we have that the area of the shaded region is 21.5 square centimeters.

Answer:

Option D