Question

A hydraulic lift is used to jack a 1170 kg car 13 cm off the floor. The diameter of the output piston is 18 cm, and the input force is 250 N.(a) What is the area of the input piston?m2(b) What is the work done in lifting the car 13 cm?J(c) If the input piston moves 13 cm in each stroke, how high does the car move up for each stroke?m(d) How many strokes are required to jack the car up 13 cm? (Include fractions of a stroke in your answer).(e) Calculate the combined work input of all of the strokes.

Answer 1

(a)
`5.45\cdot 10^(-4) m^2`

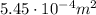
According to Pascal's principle, the pressure on the first piston is equal to the pressure on the second piston:

`p_1 = p_2\\(F_1)/(A_1)=(F_2)/(A_2)` (1)

where

F1 = 250 N is the input force

A1 = ? is the area of the input piston

F2 is the output force

A2 is the area of the output piston

The output force is just the weight of the car:

`F_2 = mg =(1170 kg)(9.8 m/s^2)=11,466 N`

The radius of the output piston is half the diameter:
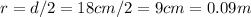`r=d/2=18 cm/2 = 9 cm =0.09 m`, so its area is

`A_2 = \pi r^2 = \pi (0.09 m)^2=0.025 m^2`

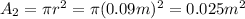
So we can solve eq.(1) for A1, the area of the first piston:

`A_1 = A_2 (F_1)/(F_2)=(0.025 m^2)(250 N)/(11,466 N)=5.45\cdot 10^(-4) m^2`

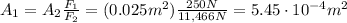
(b) 1491 J

The work done in lifting the car 13 cm is equal to the gravitational potential energy gained by the car:

`W=\Delta U=mg \Delta h`

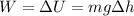
where:

m = 1170 kg is the mass of the car

g = 9.8 m/s^2

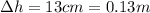`\Delta h=13 cm=0.13 m` is the increase in height of the car

Substituting,

`W=\Delta U=(1170 kg)(9.8 m/s^2)(0.13 m)=1491 J`

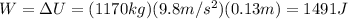
(c) 0.0028 m

Assuming the machine is 100% efficient and there is no waste of energy, the input work is equal to the output work:

`W_i = W_o\\F_1 d_1 = F_2 d_2`

where

F1 = 250 N is the input force

d1 = 13 cm = 0.13 m is the displacement of the input piston

F2 = 11,466 N is the output force (the weight of the car)

d2 is the displacement of the output piston

Solving for d2,

`d_2 =d_1 (F_1)/(F_2)=(0.13 m)(250 N)/(11466 N)=0.0028 m`

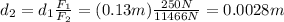
(d) 46 strokes

In order to lift the car up 13 cm (0.13 m), we have to divide this value by the displacement of the car for each stroke, so we have:

`n=(0.13 m)/(0.0028 m)=46.4 \sim 46`

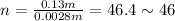
(e) 1491 J

The work done during all of the strokes is equal to the gravitational potential energy gained by the car while being lifted 13 cm, so it is equal to the value found in part b):

W = 1491 J